Angles and Parallel Lines
When parallel lines are crossed by another line (called a transversal) special pairs of angles are formed.
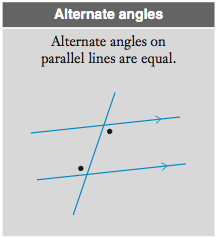
Alternate Angles
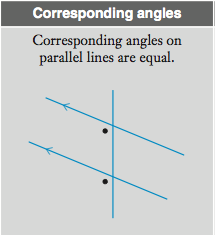
Corresponding Angles
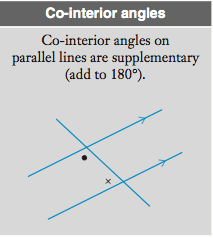
Co-interior Angles
Lets apply our knowledge of these types of angles..
1. Name an angle that is vertically opposite angle AWV
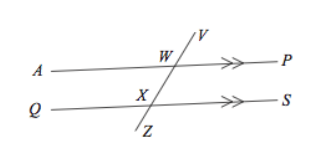
2. Name an angle that is corresponding to angle VWA
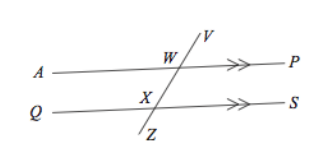
3. Name an angle that is alternate to angle QXW
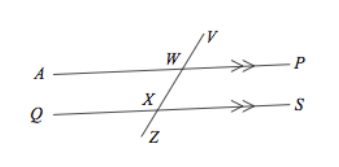
4. Name an angle that is co-interior with angle PWX
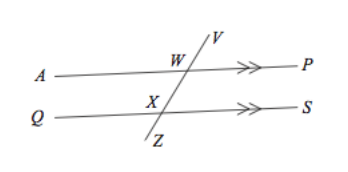
5. Name an angle that is supplementary to angle AWX
Proving that Two Lines are Parallel
To show that two lines are parallel, you must show that one of the following is true:
The following diagrams have examples of parallel lines with transversals, as well as an explanation of why they are parallel.
- a pair of alternate angles are equal
- a pair of corresponding angles are equal
- a pair of co-interior angles are supplementary
The following diagrams have examples of parallel lines with transversals, as well as an explanation of why they are parallel.
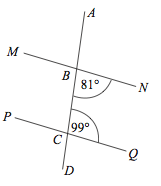
Lines MN and PQ are parallel because they have supplementary co-interior angles.
This means that a pair of co-interior angles (same side of the transversal and on the inside of the parallel lines) add up to 180°.
This means that a pair of co-interior angles (same side of the transversal and on the inside of the parallel lines) add up to 180°.
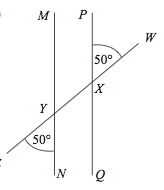
Lines MN and PQ are parallel because they have alternate angles that are equal.
This means that a pair of alternate angles (vertically opposite each other, and on different parallel lines) are equal.
This means that a pair of alternate angles (vertically opposite each other, and on different parallel lines) are equal.
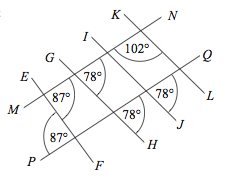
Lines MN and PQ are parallel because they have:
- equal alternate angles (on the transversal EF)
- equal corresponding angles (on the transversal GH)
